Quantum Key Distribution

The idea of quantum key distribution dates back to the seminal 1984 paper by Charles Bennett and Gilles Brassard in which they laid out a protocol for how quantum physics can be exploited to generate and securely distribute encryption keys. Basically, encryption works by taking the plain binary information and randomising/scrambling it using an encryption key. Ideally, the key itself is a completely random string of 0's and 1's and by adding the key to the binary information by XOR'ing the strings bit by bit, the randomness of the key is transferred to the information, rendering it unreadable and plain nonsens to any sniffing outsider. The encrypted information is commonly referred to as the crypotext.

If, say, a sender Alice and receiver Bob are making a secure data transmission using, as most other people in the world, AES encryption then the very same encryption key is used both to encrypt the information and to decrypt it again. This kind of protocol is called symmetric encryption. Obviously, for it to work and maintain information privacy, the encryption key must be shared by both Alice and Bob and must not under any circumstance be known to anyone else. This makes secure key distribution a vital part of any symmetric encryption scheme.

Let's return to Bennett and Brassard. What they showed in 1984 was that the indeterminate and probabilistic nature of quantum physics can be exploited for cryptography, in particular for quantum key distribution (QKD). The scheme they devised has afterwards become known as the BB84 protocol and has been a key driver for the development of quantum cryptography technologies because it illustrated how fundamental quantum physics principles enable secure key distribution. Since 1984, a number of different protocols have seen the light of day and QKD has now matured to be an emerging technology, on the verge to large-scale implementation in the global society. The increasing threat from cyber attacks along with steady progress in quantum computing have been and remain strong motivating factors for the fast development of QKD. Most recently, continuous variable protocols, as is the focus of CryptQ, have gained momentum due to their technological simplicity over discrete variable (DV) ones.

"When elementary quantum systems, such as polarised photons, are used to transmit digital information, the uncertainty principle gives rise to novel cryptographic phenomena unachievable with traditional tranmission media, e.g. a communications channel on which it is in principle impossible to eavesdrop without a high probability of disturbing the transmission in such a way as to be detected."

- C. Bennett & G. Brassard, 1984

In the end it's all about Heisenberg's uncertainty principle and the no-cloning theorem. Heisenberg's uncertainty principle tells us that at the quantum level certain physical properties of an object cannot be defined simultaneously and that translates into a fundamental uncertainty - quantum noise - on how well we can measure those properties at the same time. Physical properties showing this kind of uncertainty are known as non-commuting observables. For light, examples are the polarisation observables of a single photon (this is the degree of freedom used in BB84) and the amplitude and phase of a continuous laser beam (that's the relevant one for CV-QKD).

Classical optical communication

Before we go deeper into it, let's take a brief detour to classical optical communication. The world is interconnected with optical fibres that allow us to transmit digital information over long distances and with high speed using laser light as the carrier medium. A characteristic of laser light is that it is single frequency and we can think of it as a wave oscillating with stable frequency and phase. This type of optical state is also known as a coherent state. By applying modulations to the light wave that wiggles its amplitude (AM) and phase (PM) we can create new coherent states with precisely controlled amplitude and phase by tuning the respective modulation strengths. In this way we can build up an alphabet of optical states and use them to encode information. This is what's done in e.g. Quadrature Phase-Shift Keying (QPSK).

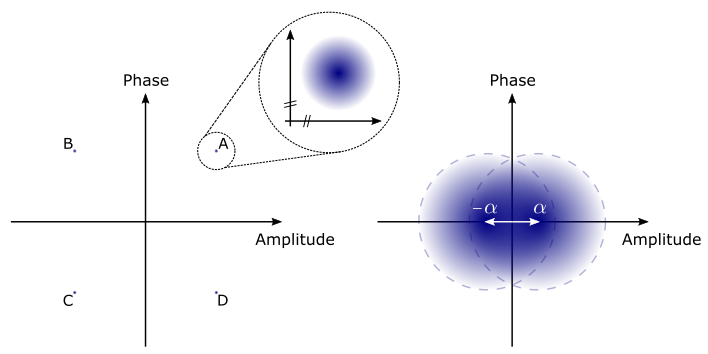
Classical optical communication uses optical modulation to generate an alphabet of distinguishable optical states for encoding of information (left). When the modulation is weak, quantum noise makes the states overlap and hence partly indistinguishable (right). This is exploited for CV-QKD. 

Useful noise

Now, if we zoom in on the alphabet states we notice that they are in fact not dots but blurred blobs. This "blur" is quantum noise, and it is a result of Heisenberg's uncertainty relation between the amplitude and phase quadratures. In optical telecommunication we don't care about this noise. We just modulate strongly enough that the alphabet states are effectively point-like and can be perfectly discriminated.

For QKD, we do exactly the opposite. Using only weak modulations, we create states that are not indistinguishable because their quantum noise overlaps. In the simplest case, we generate just two different states with a slight separation, as illustrated above - the one state representing a binary "0" and the other a "1". 

A QKD setup consists of a transmitter and a receiver. The transmitter generates a long stream of quantum states, in each case randomly picking a "0" or "1" encoding, and transmits that to the receiver. On the receiver side, a random choice is made on what property to measure for each of the exchanged states and the results are logged. In the event that the receiver measurement is compatible with the transmitters encoding, the encoded bit value is faithfully recovered. In the opposite case, the receiver generates a random bit. Following the exchange of quantum states, transmitter and receiver communicate via an authenticated classical channels, exchanging information about how the states were encoded and measured. The bit strings on either side are then decimated, keeping only those corresponding to compatible encoding and measurement choices.

The fact that the transmitted states cannot be discriminated means that a hacker also cannot tap into the transmission line and figure out the encryption key that the two parties are going to use when they start transferring data. And if he does try, he will always leave a noticeable trace. Consider the simplest type of attack the hacker can do: intercept and resend. In this case he does just like the receiver - he measures the states sent by the transmitter randomly, records the results, and then prepares states identical to what he has measured and resend them to the receiver. However, the states from the receiver are effective superpositions of "0" and "1" and each measurement will yield random results. With a certain probability he will get the same result as recorded by the transmitter and with another probability the opposite. When the hacker intercepts and resends he breaks the original probability distribution for transmitter and receiver to obtain identical/opposite results and that change can be detected. And that is exactly what the transmitter and receiver stations will do in the post-processing step. As soon as a discrepancy is flagged the key exchange is aborted and restarted.